IEEE 754와 부동소숫점, 10진수<->2진수 변환 등을 다룬 글
> 시간나면 꼭 한번 읽어보기
: What Every Computer Scientist Should Know About Floating-Point Arithmetic
실수를 나타내는 방법 중 Scientific notations이란 것이 있다.
소숫점 왼쪽에 숫자가 하나만 있는 경우를 말한다. ex) 2.17x10^6, 0.7x10^(-1)
이런 Scientific notations 중 소숫점 왼쪽에 0이 아닌 숫자가 오는 경우를 Normalized 됐다고 한다.
이진수로 표현된 실수를 모두 Normalized form으로 변경하면 모두 아래와 같이 정형화(?)된다.

우리는 모든 실수를 위와 같이 표현할 수 있는 것이다.
어떻게 저장할까? 이미 알고있는 값인 1과 2는 굳이 저장할 필요가 없다.
즉, x와 y만 저장하면 된다.
이 x와 y를 저장하는 법을 IEEE 754에서 두가지 방법으로 정의한다.(더 있긴 함)


왼쪽처럼 32비트 공간을 사용하는 것을 Single Precision, 오른쪽처럼 64비트 공간을 사용하는 것을 Double Precision이라한다.
exponenet는 2의 지수인 y를 저장하고, fraction(mantissa, significand)는 소숫점 오른쪽의 x를 저장한다.
(위 형태로 표현된단거고, 메모리에 저장될땐 당연히 endian이 반영된다. 참고)
> Single Precision
sign : 1-bit
exponent : 8-bit
fraction : 23-bit
위와 같이 할당해 사용한다. exponent를 8밖에 안준 이유는 지수가 2^8만 돼도 충분히 큰 숫자를 표현할 수 있기 때문이다.(헷갈리지 말자 2의 "지수인 y"가 2^8이 되는거다.)
exponent와 fraction은 서로 한쪽이 늘면 한쪽이 줄어드는 trade-off이긴 한데, 전문가들이 모여서 얘기한 결과 저렇게 exponent는 8비트 정도만 줘도 충분히 큰 숫자를 표현할 수 있고, 나머지 숫자들로 precision을 높이는걸 선택한 것이다.
쓸 수도 없는 큰 숫자를 표현하기 위해 exponent를 공평하게 15비트 정도 나눠줄 필욘 없단 뜻이다.
> Double Precision
sign : 1-bit
exponent : 11-bit
fraction : 52-bit
위와 같이 할당해 사용한다. 마찬가지로 단정밀도에 비해 size는 두배가 늘었는데 exponent를 11-bit밖에 안준 이유는 지수가 2^11만 돼도 충분히 큰 숫자를 표현할 수 있기 때문이다.(거의 플마 2^1000 까지 표현됨..)
Biased Notation
기본적으로 FP(Floating Point)는 IEEE 754에 의해 sign-magnitude 방식으로 표현된다. (보면 알겠지만 sign 비트가 따로 떨어져있음)
exponent 부분은 특별히 Biased Notation이란 표현법으로 표현된다.
음수를 2의 보수로 표현했던 정수와 달리,
single precision에서 y에 들어가는 숫자는 10진수 127이 더해져서 exponent에 저장된다.
exponent 값이 0과 255인 경우는 특수한 경우이므로, 1부터 254까지 일반 exponent가 사용한다.
127이 더해져서 저장되니 실제 y에 올 수 있는 값은 -126~127까지이다. (더했을때 1~254 범위에 들어와야되니까)
즉 exponent 값만 보자면, exponent가 1이면 이는 사실 가장 작은 음수인 -126이고, exponent가 254이면 가장 큰 양수인 127이다. 2의 보수와는 달리 직관적으로 쭉 저장이된다.
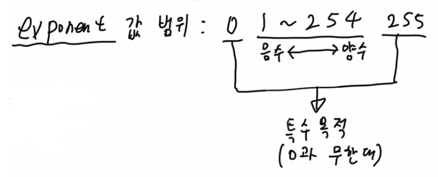
Double-Precision에선 Bias가 1023이다.
굳이 bias로 표현하는 이유는 IEEE 754 설계자들이 interger sorting 연산을 FP에도 적용하고 싶었기 때문이다.
2의 보수로 표현하면 일반 sorting으론 음수 양수 구분이 안돼 결과가 이상하게 나온다.
하지만 위처럼 bias를 더해서 표현하면 단순 비교로 누가 더 큰지를 알 수 있다.
(sign을 제일 앞에 보낸 것도 바로 대소비교 하기 위해서 라고 하네)
> 특수 숫자
1. Exponent: 0, Fraction: 0 --> 0
2. Exponent: 255, Fraction: 0 --> Infinity
3. Exponent: 255, Fraction: Nonzero --> NaN
4. Exponent: 1-254, Fraction: anything --> normal FP number
5. Denormalized number : 정상범위보다 작은 숫자 표현할때 사용.. 자세한건 여기
참고로 1번과 2번은 sign에 따라 플러스0, 마이너스0, 플러스inf, 마이너스inf 를 나타낸다.
NaN은 0/0 같은 Invalid 연산시 결과로 나온다. NaN은 그런 특수 상황을 programmer가 나중에 판단하고 테스트 할 수 있도록 해준다.
> Overflow & Underflow
Overflow : exponent가 field에 들어갈 수 없을 정도로 큰 경우 (fraction은 상관 X)
Underflow : exponent가 음의 방향으로 너무 커서 field에 들어갈 수 없는 경우 (fraction은 상관 X)
(255 infinity가 overflow를 표현하는 거라고 하네,, 그러니 exponent가 254 넘어가면 overflow 인듯)
(underflow는 denormalized number도 있고하니 denormalized 범위도 넘어가야 underflow라고 하나?? 좀 애매하긴 함. underflow 참고)
overflow/underflow 발생하면 exception이나 interrupt를 raise 할 수도 있고 안할수도 있다.
RISC-V에선 딱히 exception을 raise하지 않고, floating-point control and status register(fcsr)이란 것을 software가 읽어서 알아서 판단하도록 한다.
> FP addition
1. decimal point 위치를 맞춘다.(여기선 지수가 작은 놈을 큰놈한테 맞췄다.)
2. significand 끼리 더한다.
3. Normalize 한 뒤 overflow/underflow 여부를 확인한다.
3-1. overflow/underflow라면 예외로 빠진다.
4. 저장 공간 크기에 맞춰 Round한다.
4-1. 여기서 round 후에 normalize된게 깨졌다면 다시 3번으로 돌아가야한다.(loop 구성)
4-2. (round라는게 말은 쉽지만, 유한 자원에서 정확하게 하기는 쉽지않다. 그래서 IEEE754에선 덧셈 연산시 뒤에 guard와 round 라고 하는 비트 두개를 붙여서 사용하도록 한다.)
1번 과정에서 둘의 exponent 차이가 많이나면 저렇게 하면 안된다. 소숫점 위치 맞추다가 significand 다 날릴 수도 있다.
애초에 이렇게 제한된 크기에서 엄청 큰 숫자와 엄청 작은 숫자 덧셈 결과를 표현할 수 있는지 의문이긴 하네
> FP addition Hardware

위 FP 덧셈 과정을 그대로 HW에 구현한 것이다.(하나하나 따라가보면 이해됨)
보면 알겠지만 정수 덧셈에 비해 회로가 꽤 복잡하다. 그래서 보통 CPU에는 Floating Point 연산을 처리하는 Unit이 따로 있다.
Fallacies & Pitfalls
실제 세상의 무한한 숫자와 컴퓨터 세상의 유한한 숫자 표현법 사이 충돌로 인해 주로 오류가 생긴다.
> Fallacies(오류)
1. Just as a left shift instruction can replace an integer multiply by a power of 2, a right shift is the same as an integer division by a power of 2.
: 양수에선 어느 정도 맞는 얘기일 수도 있다. 하지만 양수여도 bit 공간 제한이 있으니 짤려 나갈 위험이 있다. 음수면 right shift 연산시 arithmetic 버전을 사용해야만하고, 결과도 정확하지 않을 수 있다.(ex. -5를 우측으로 arithmetic shift 2번 시키면 결과는 -2가 나옴. -1이 나와야지)
2. Parallel execution strategies that work for integer data types also work for floating-point data types.
: 일단 아래 Pitfall 항목에 있듯이 floating point는 덧셈에서 결합 법칙이 성립하지 않으므로 덧셈만 한다고 해도 여러 프로세서를 동시에 활용하면 결과가 달리 나올 위험이 있다. 심지어 어떤 parallel computers는 현재 돌아가고 있는 프로그램에 따라 특정 프로그램에 프로세서 수를 다르게 할당해주기도 한다. 즉, 같은 프로그램이더라도 FP를 병렬로 처리한다면 매번 결과가 다를 위험이 있다는 말이다. 그러니 FP 숫자를 병렬처리하려면 확실히 검증해야한다. 이런 issue를 numerical analysis라고 하는데 책 한권으로 따로 뺄 정도의 분야이다. 즉 FP를 병렬로 처리는 해야되는데 처리하기가 쉽지는 않다. 그래서 LAPACK이나 ScaLAPAK 같은 sequential과 parallel을 모두 지원하는 검증된 라이브러리가 유명한 이유 중 하나가 이것이다.
3. Only theoretical mathematicians care about floating-point accuracy.
: 1994년 11월 신문 헤드라인을 보면 위 문장이 잘못됐다는걸 알 수 있다. 그 당시 Intel의 pentium이 FP 나눗셈 연산을 할때 잘못된 결과를 낼 수 있다는 점이 드러났다. 자세한 설명
물론 이 오류가 상당히 낮은 확률로 발생하는 것이긴 했으나, Intel은 이때의 부주의로 인해 5억 달러 가량 손실을 봤다.
> Pitfalls(위험)
1. Floating-point addition is not associative.
: FP 덧셈연산에선 항상 결합 법칙이 성립하지는 않으니 주의해라.(이 또한 유한한 자원때문인데) 위에서 말했듯이 FP 덧셈 연산에서 처음에 소숫점 위치를 맞춰주고 덧셈을 해야한다. 그렇기에 두 숫자사이 exponent 차이가 크다면, align을 하다가 significand 부분이 다 날아가서 사실상 0을 더하는 꼴이 될 수 있다. 예시로 단정밀도에서 1.5x10^38과 1.0을 더하면 1.0x10^0을 10^38까지 올리다가 1이 없어지므로 더한 결과는 1.5x10^38이 된다.
a=1.5x10^38, b=-1.5x10^38, c=1.0이라고 해보자. (a+b)+c 는 a+b인 0과 1.0을 더하니 1.0이지만, a+(b+c)는 1.5x10^38과 b+c인 -1.5x10^38을 더하니 0이 나온다.
> 번외
> Floating-Point Instructions in RISC-V
수업에선 다루지 않은 내용이지만 책엔 있어서 간단하게 한번 정리해볼까한다.
우선 RISC-V는 floating point를 위한 register를 따로 제공한다. f0-f31로 지칭한다. 얘네를 이용해서 실수연산 명령어를 사용한다.
기본적인 기능은 정수와 같다. add, sub, mul, div, ld, sd, ...
단 저기서 앞에 "f"를 붙이고, 뒤에는 ".s" 혹은 ".d"를 붙인다. 뒤에붙는 s와 d는 각각 single precision과 double precision을 말한다.
ex) fadd.s, fsqrt.d
단, load나 store 연산은 byte 수로 단정밀도, 배정밀도를 생각하므로 뒤에 .s .d를 안붙여도 된다.
flw를 쓰면 자동으로 single-precision으로 값을 불러오고, fsd를 쓰면 자동으로 double-precision으로 값을 메모리에 작성한다.
'수업 > Computer Architecture' 카테고리의 다른 글
| [Computer Architecture] Processor - 1 (0) | 2022.11.08 |
|---|---|
| [Computer Architecture] Memory Hierarchy (0) | 2022.10.20 |
| [Computer Architecture] Arithmetic for Computers(1) (0) | 2022.10.13 |
| Language of the Computer (5) | 2022.09.14 |
| Introduction (3) | 2022.09.13 |